Studienblog

Korrelation

Die Korrelation ist eines der wichtigsten und am häufigsten genutzten statistischen Maße. In vielen Studien ist sie der entscheide Kennwert, es ist entsprechend wichtig, das Maß in seinen Grundzügen zu verstehen. Daher konzentrieren wird uns in diesem Beitrag alleine auf das Zusammenhangsmaß, dessen Bedeutung und Interpretation. Wir wollen ihnen eine kleine Hilfe geben, um sich in der Welt der empirischen Forschung besser zurecht zufinden und sich selbst eine Meinung bilden zu können.

Veranschaulichung der Korrelation

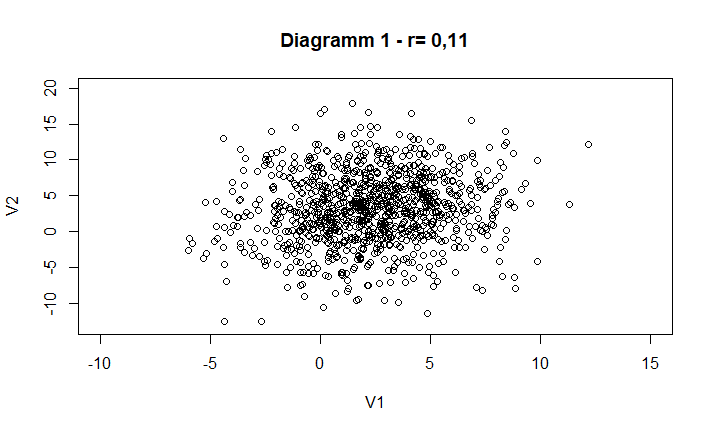
Die Langlebigkeit und die Persönlichkeitsdimension „Gewissenhaftigkeit“ korrelieren mit r= 0,11 (Bogg & Roberts, 2012; Kern & Friedman, 2008). Wer nicht weiß, für was „r“ hier steht, ist nun keinen Deut schlauer als zuvor. „r“ ist die Abkürzung für den Korrelationskoeffizient und gibt als solcher den Grad der Korrelation oder auf Deutsch, den Grad des Zusammenhangs an (Field, Miles, & Field, 2013). Der deutsche Begriff, wie so oft, erklärt bereits in seinen Grundzügen was wir mit Korrelation meinen: Zusammenhangsmaß. Ein Maß, wie z.B. Meter, Kilo oder Minuten, welches uns sagt, wie groß der Zusammenhang zwischen zwei Faktoren, zwei Variablen ist.

Die korrelativen Variablen

Bei unserem Beispiel lauten die beiden Variablen Langlebigkeit und „Gewissenhaftigkeit“. Genauso wie bei Metern kann ein Mensch ganz unterschiedlich gewissenhaft sein. Manche sind z. B. ein wenig, ein bisschen mehr, mittelstark, stark oder sehr stark gewissenhaft. Es gibt also nicht gewissenhafte Menschen auf der einen Seite und nicht gewissenhafte auf der anderen. Stattdessen gibt es unzählige Ausprägungen, wie gewissenhaft man sein kann. Ähnlich ist es beim Alter bzw. der Langlebigkeit. Die Langlebigkeit, gemessen in einer Zeiteinheit wie Minuten, kann ganz unterschiedlich ausfallen. Es gibt nicht nur die Langlebigen und die Kurzlebigen.

Unsere Forschungsfrage ist: Existiert ein statistischer Zusammenhang zwischen dem Grad der „Gewissenhaftigkeit“ und der Langlebigkeit eines Menschen, sowie, ist dieser Zusammenhang positiv oder negativ.

Implikationen einer Korrelation

Wenn ein Zusammenhang besteht, dann würde dies bedeuten, dass sich mit jeder Erhöhung der Variable „Gewissenhaftigkeit“ sich auch die Variable Langlebigkeit um einen vergleichbaren Anteil verändert. Ist der Zusammenhang hierbei positiv, so bedeutet dies, dass eine Erhöhung in „Gewissenhaftigkeit“ zu einer Erhöhung der Langlebigkeit führt. Umgekehrtes gilt für einen negativen Zusammenhang. Eine Erhöhung in „Gewissenhaftigkeit“ verringert die Langlebigkeit. Was wir nun also brauchen ist eine statistische Methode um diesen Zusammenhang zu berechnen – die Korrelation.

Verwechslung der Korrelation mit der Regression

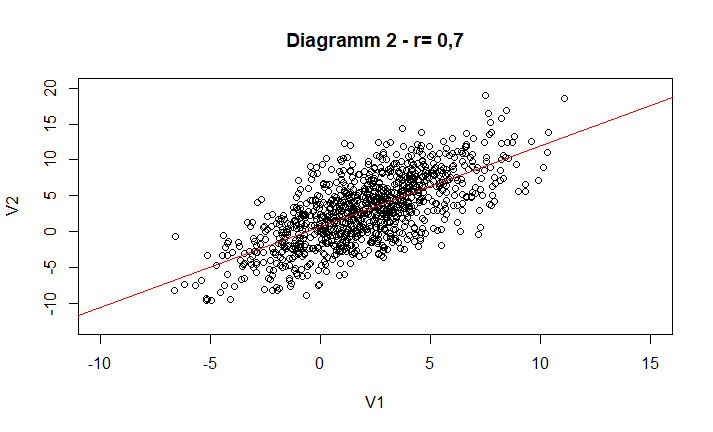
Hier besteht eine Verwechslungsgefahr mit dem Regressionskoeffizienten. Dieser gibt an, wie stark sich eine Kriteriumsvariable, in unserem Beispiel die Langlebigkeit, verändert, wenn sich die Prädiktorvariable („Gewissenhaftigkeit“) um eine Einheit verändert. Wenn sich „Gewissenhaftigkeit“ z.B. um eine Einheit erhöht, dann würde uns der Regressionskoeffizient sagen, um wie viel sich die Langlebigkeit erhöht. Mit Hilfe der Regression könnte man also die Langlebigkeit anhand der „Gewissenhaftigkeit“ vorhersagen. Wie stark der Effekt von „Gewissenhaftigkeit“ ist kann man am einfachsten anhand eines Diagrammes ablesen. Das Diagramm 2 stellt eine Regressionsgerade dar. Im Vergleich zu Diagramm 3 ist die Gerade weniger steil. Den Grad der Steilheit der Gerade wird durch den Regressionskoeffizienten bestimmt, nicht vom Korrelationskoeffizienten (für mehr Infos rund um die Regression klicke hier). Die Streuung der vielen Punkte um die Gerade hingegen wird nicht vom Regressionskoeffizienten angegeben.

Diese Streuung ist letztendlich das, was vom Korrelationskoeffizienten angegeben wird. Ist ein Zusammenhang perfekt (r= 1), dann gäbe es die Streuung bei Diagramm 2 und 3 nicht. Jeweils würde sich eine Linie ergeben. Den Grad der Steigung dieser Linie, wird allerdings nicht von der Korrelation angegeben. Da bei der Korrelation keine Gerade berechnet wird und diese bei Darstellungen von korrelativen Zusammenhängen in aller Regel fehlt, kann man sich die Stärke einer Korrelation auch mit der Kompaktheit einer Punktwolke, also den eingezeichneten Koordinaten, vorstellen. Wenn die eingezeichneten Koordinaten eng bei einander liegen, liegt eine hohe Korrelation vor, wenn sich eine sprichwörtliche Wolke bildet, da jede Koordinate relativ weit von der nächsten entfernt ist, so ist die Korrelation niedrig (siehe Diagramm 4 und 5).

Interpretation von Korrelationen

Diagramm 5 zeigt tatsächlich eine Korrelation von r= 0,11 dar. Allerdings handelt es sich hier nicht um die originalen Daten der Studie zu Langlebigkeit und der Persönlichkeit. Es handelt sich um eine Simulation von Daten, die eine Korrelation von r= 0,11 ergeben und dient hier nur dem Zweck der Veranschaulichung. Wie man erkennen kann, ist bei einer so niedrigen Korrelation mit dem bloßen Auge kaum ein Zusammenhang zu erkennen. Mathematisch jedoch ist ein Zusammenhang feststellbar. Trotzdem stellt sich nun die Frage, ob der Zusammenhang nicht viel zu klein ist, um wirklich für die Langlebigkeit eines Menschen relevant zu sein. An dieser Stelle muss man ein klares „Jaein“ geben. Statistisch gesehen handelt es sich nur um einen kleinen Zusammenhang. Bedenkt man jedoch, dass die Geltung der Big-Five Taxonomie bisher für die meisten westlichen Länder insbesondere Deutschland, England, die Niederlande und auch für die USA festgestellt werden konnte, ist der Zusammenhang in tatsächlichen Zahlen durchaus relevant. Ein nicht ganz sauberer, jedoch anschaulicher Vergleich ist vielleicht die Vorstellung, dass 0,1% von 1000 Personen lediglich 1 Person ist. Von 80 Millionen hingegen sind 0,1% 80.000 Personen. Dies ist nicht der Effekt von der Persönlichkeitsdimension “Gewissenhaftigkeit“, jedoch zeigt das Beispiel, das kleine statistische Kennwerte auf die tatsächliche Anzahl an Personen angewendet für viele Menschen relevant ist. 80 Millionen ist übrigen in etwa die Einwohnerzahl Deutschlands.

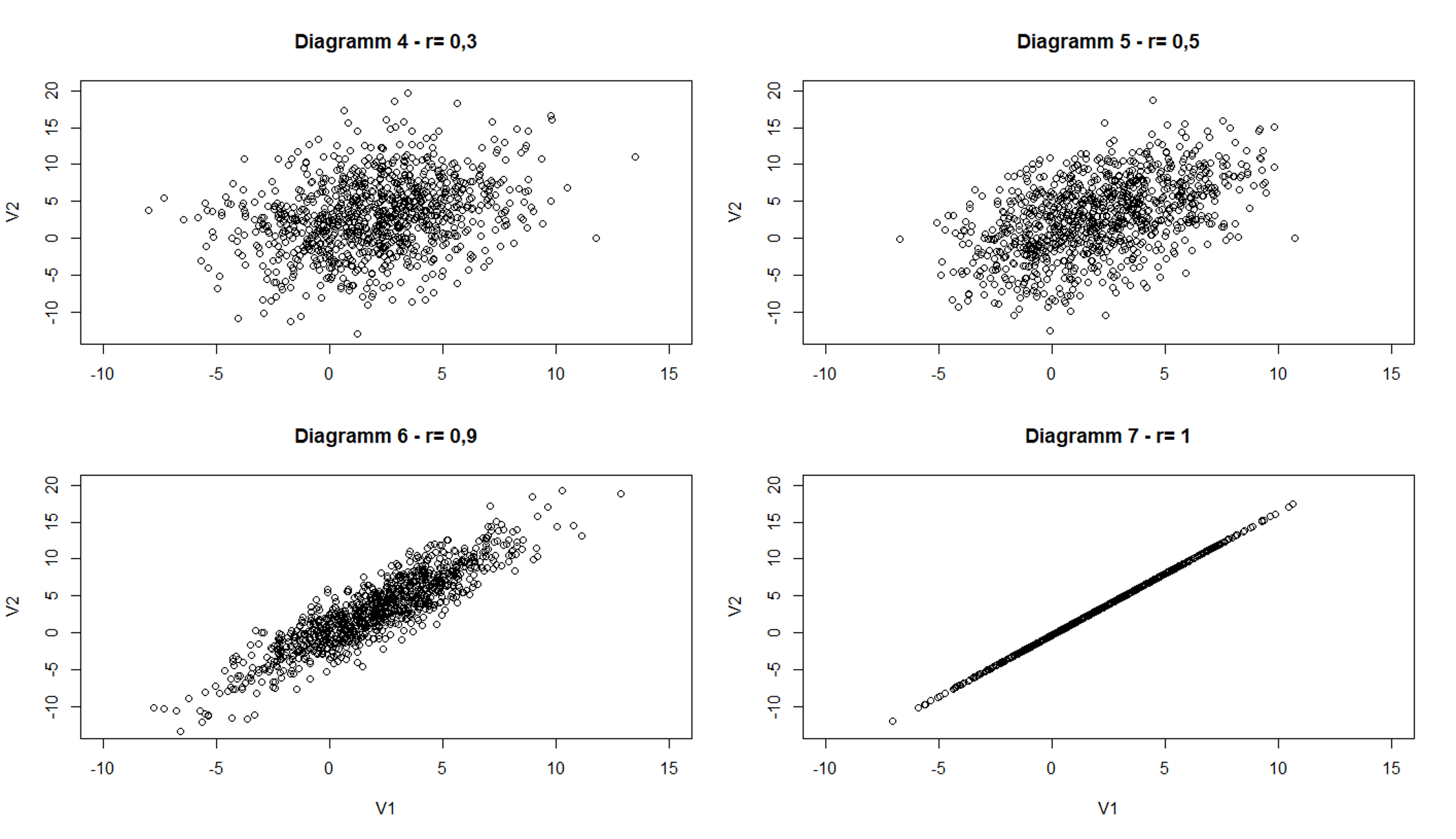
Alle statistischen Maße sollten also im Rahmen des thematischen Kontextes betrachtet werden. Dass man bei einer Korrelation von r= 0.1 dennoch von einer schwachen Korrelation spricht, liegt an den Interpretationsmaßstäben, auf die man sich in der Psychologie geeinigt hat. Eine kleine Korrelation liegt bei den besagte r= 0,1, eine mittelstarke Korrelation bei r= 0,3 (Diagramm4) und eine starke Korrelation bei r=0,5 (Diagramm 5). Simulierte Daten mit einer Korrelation von r= 0,9 und r= 1 sind auf den Diagrammen 6 und 7 erkennbar.

Nach rechts scrollen